
Любознательность порой приводит людей к неожиданным открытиям. Даёт ценный опыт и раздвигает горизонты познания. Так и моё небольшое желание найти оптимальный путь получения цвета по шестнадцатеричному коду вылилось в эпопею с изучением алгоритмов, проведением тестов производительности и наконец, выкладыванием моей первой библиотеки на Github. Итак, вот с чего всё начиналось…
Не секрет, что в программировании принято обозначать цвета кодом. Это либо шестнадцатеричное шестизначное число, либо три десятичных числа (RGB) от 0 до 256. Эти числа легко преобразуются друг в друга и представляют из себя сочетание трёх базовых цветов (красный, зелёный и голубой) различной насыщенности. Простой подсчёт даёт понять, таких сочетаний более 16-ти миллионов. Однако имена дали лишь паре сотен из них. Все остальные — безымянные. Однако, это не мешает дизайнерам использовать безымянные цвета для оформления веб-страниц. Вот выдумщики. И как же мне быть, если я хочу узнать, какой цвет использовался при оформлении сайта? Как найти ближайший именованный цвет?
Первой идеей был парсинг сайтов. Яндекс без проблем выдаст ближайший именованный цвет по его коду. Да и другие сайты можно найти, которые без проблем выдают ближайшие цвета. Однако, когда нужно выяснить ближайшие цвета для десятка стилей, да ещё и автоматизировать это, такой подход не годится. Большинство сайтов блокируют слишком частые запросы к ним, а выдаваемые цвета (как позже выяснится) не так уж и точно определяются. Так может стоит сделать небольшую библиотеку, содержащую все известные цвета и просто выдавать ближайший подходящий? Так и было решено сделать. Оставался один вопрос. Какой цвет считать ближайшим?
При подробном рассмотрении вопроса выяснилось, что RGB-цвет подобен точке в трёхмерной системе координат. А значит вопрос нахождения ближайшего цвета сводился к чтению координат(RGB) известных цветов и нахождению расстояния между каждой из известных точек и искомой. Так появился первый метод первого класса ColorPoint:
protected static double calculateDistance(ColorPoint one, ColorPoint two) {
return Math.sqrt(Math.pow(one.getRValue() — two.getRValue(), 2) +
Math.pow(one.getGValue() — two.getGValue(), 2) +
Math.pow(one.getBValue() — two.getBValue(), 2));
}
Корень из суммы квадратов разности соответствующих координат. Неплохой вариант, но насколько он производителен? Что если подсчитать наименьшее из двухсот расстояний — не лучший вариант? Поиск в сети навёл меня на сайт RoboWiki, где я нашёл несколько реализаций алгоритма поиска наименьшего расстояния между точками. Оказалось, эта проблема решается методом перелива(или методом вёдер) с помощью построения kd-дерева. Я не стал углубляться в теорию. Разобрав предложенные варианты, я написал нечто подобное.
Суть метода вёдер заключается в том, что все известные точки мы раскладываем по так называемым вёдрам (это области пространства в пределах определённых координат). И когда нам надо найти ближайшую — мы сперва определяем, в каком ведре (области пространства) эта точка находится, а потом вычисляем расстояние лишь до тех точек, которые находятся в том же ведре. При этом, если кратчайшее расстояние до точки больше, чем расстояние до границы ведра, то мы ищем ещё и в соседних вёдрах. Конечно, точек в пространстве гораздо больше, чем цветов, так что моя реализация получилась чрезмерно упрощённой.
Итак, для начала я создал три класса. Базовый — TableOfColor – таблица цветов. Вспомогательный — BucketOfColor – ведро с цветами. И ещё один, вполне очевидный — ColorPoint – точка-цвет. Не буду углубляться во вспомогательные классы, вы можете найти их на моей страничке в Github. Разберу лишь алгоритм распределения цветов по вёдрам. Класс ColorTable имеет следующие поля:
public class TableOfColor {
private final Locale locale;
private final String ymlFile;
private final List<ColorPoint> colors;
private final List<BucketOfColor> buckets = new ArrayList<>();
private int[] startPoint = new int[]{0, 0, 0};
private int[] endPoint = new int[]{256, 256, 256};
private int maxPointsCount;
Точки берутся из yaml-файла, название которого зависит от языка создаваемой таблицы. ru.yml, en.yml и т. д. Других таблиц я не создавал, но вполне могу заняться, если будет желание и время. Все строки из файла конвертируются в цвета и помещаются в общий список. Кроме того, создаётся список вёдер, в каждом из которых также есть свой список принадлежащих ему точек. Точки постепенно распределяются по вёдрам. Если ведро заполнено, то вместо него создаются два ведра и точки распределяются между ними. Вот как выглядит конструктор:
public TableOfColor(Locale locale) {
this.maxPointsCount = 16;
this.locale = locale;
this.ymlFile = locale.getLanguage() + «.yml»;
this.colors = extractYml(this.ymlFile);
this.buckets.add(new BucketOfColor(startPoint, endPoint));
distributePoints(colors);
}
При распределении точек я исходил из предположения, что они распределены неравномерно по изначальному кубу? Ограниченному координатами {0,0,0} {256,256,256}. Поэтому и использовался метод перелива.
Если кратко, логика работы такая. Сперва вызываем метод distributePoints:
private void distributePoints(List<ColorPoint> points) {
points.forEach(point -> {
BucketOfColor bucket = findBucket(point); //для каждой точки находим ведро
bucket.addColorPoint(point); // и добавляем туда точку
});
}
Во время поиска подходящего ведра мы одновременно проверяем, не заполнилось ли оно и если заполнилось до значения maxPointsCount – делим ведро надвое по оси, где разброс точек максимален.
private BucketOfColor findBucket(ColorPoint point) {
BucketOfColor resultBucket = buckets.stream()
.filter(bucket -> bucket.isContainPoint(point))
.findFirst().orElseThrow(); // находим ведро для точки
if (resultBucket.getSize() < maxPointsCount) {
return resultBucket;
} else {
splitBucket(resultBucket);
return findBucket(point); // рекурсия иногда бывает полезна
}
}
При делении ведра надвое мы убираем старое из списка, а его точки делим между om rolex submariner mens rolex calibre 2836 2813 116613lb 97203 15mm two tone двумя новыми, рекурсивно вызывая метод distributePoints:
private void splitBucket(BucketOfColor resultBucket) {
int bestAxis = resultBucket.getBestColorAxis();
int newBound = resultBucket.getBoundPlane(bestAxis);
int[] leftBoundCoordinates = new int[3];
int[] rightBoundCoordinates = new int[3];
resultBucket.getStartCoordinates();
for (int j = 0; j < 3; j++) {
leftBoundCoordinates[j] = resultBucket.getEndCoordinates()[j];
rightBoundCoordinates[j] = resultBucket.getStartCoordinates()[j];
}
leftBoundCoordinates[bestAxis] = newBound;
rightBoundCoordinates[bestAxis] = newBound + 1;
BucketOfColor leftBucket = new BucketOfColor(resultBucket.getStartCoordinates(), leftBoundCoordinates);
BucketOfColor rightBucket = new BucketOfColor(rightBoundCoordinates, resultBucket.getEndCoordinates());
List<ColorPoint> reDistributedPoints = resultBucket.getBucketPoints();
buckets.add(leftBucket);
buckets.add(rightBucket); // добавляем новые вёдра
buckets.remove(resultBucket); // удаляем старое ведро
distributePoints(reDistributedPoints);
}
Что же, основная работа сделана. Сам метод поиска, как и все остальные, можно найти на страничке библиотеки на гитхабе. Они довольно банальны. Однако заслуживают жизни. Применение библиотеки наглядно показало, что многочисленные сайты(в т.ч. Яндекс) вычисляют ближайший цвет недостаточно точно. Поэтому я оформил эти классы библиотекой. К счастью, я уже умел это делать.
Но ещё одна мысль грызла мою душу. Каков же оптимальный размер ведра, при котором библиотека показывает наилучшее быстродействие. Пришлось не только добавить в проект бенчмарк JMH, но и временно добавить конструктор с указанием размера ведра.
public TableOfColor(int maxPoints){
this.maxPointsCount = maxPoints;
this.locale = new Locale(«ru»);
this.ymlFile = locale.getLanguage() + «.yml»;
this.colors = extractYml(this.ymlFile);
this.buckets.add(new BucketOfColor(startPoint, endPoint));
distributePoints(colors);
}
Для теста я сконфигурировал JMH следующим образом:
@BenchmarkMode(Mode.AverageTime) // нас интересует среднее время
@Warmup(iterations = 5) // несколько итераций будет занимать прогрев
@Measurement(iterations = 50, batchSize = 20) //каждый метод вызовем 20 раз для точности
@OutputTimeUnit(TimeUnit.MILLISECONDS) // время будем считать в миллисекундах
@State(Scope.Benchmark) // эта аннотация подразумевает несколько тестов одного параметра
public class MicroBenchmark {
@Param({«10», «15», «20», «25»}) // значения параметров для теста
int maxPointCount;
List<String> hexes = new ArrayList<>();
public static void main(String… args) throws IOException, RunnerException {
org.openjdk.jmh.Main.main(args);
}
Как и в Junit-тестах, есть аннотация для предварительной настройки, где мы можем насоздавать рандомных точек, которые будем потом проверять.
@Setup
public void init() {
for (int i = 0; i < 10; i++) {
hexes.add(String.format(«%06x», new Random().nextInt(0xffffff + 1)));
}
}
Тестовый метод выглядел вот так.
@Benchmark
@Fork(1)
public void testBucketCount(MicroBenchmark state) {
TableOfColor colors = new TableOfColor(maxPointCount);
for (int i = 0; i < 10; i++) {
colors.findNamedColorWithoutBuckets(hexes.get(i));
}
}
Результаты показали практически равное время для диапазона 10-20 и всего лишь немного большее для остальных значений.
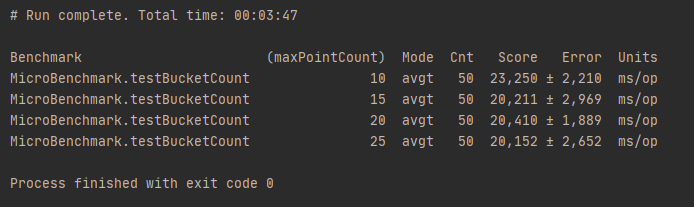
Более подробный тест показал, что разброс минимален и сильно зависит ещё и от точек (ведь мы расширяем границы поиска для некоторых случаев)
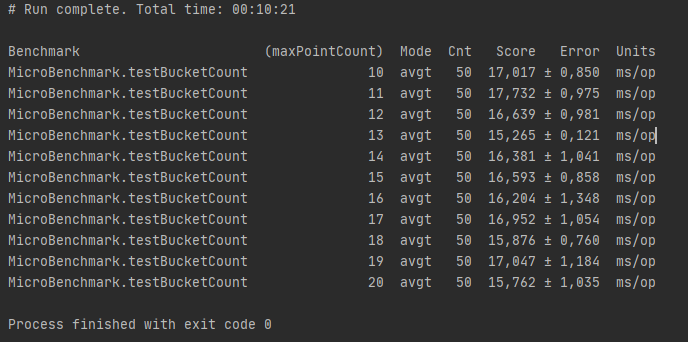
Поэтому я выбрал размер ведра произвольно и сделал равным 16-ти.
После проведённых тестов возникла идея проверить, действительно ли поиск методом вёдер эффективнее обычного перебора. Я добавил метод поиска цвета без использования вёдер и ещё один конструктор своему классу. Без первоначального распределения цветов.
public TableOfColor(){
this.locale = new Locale(«ru»);
this.ymlFile = locale.getLanguage() + «.yml»;
this.colors = extractYml(this.ymlFile);
}
Тесты проводил вот таким образом:
@Benchmark
@Fork(1)
public void testGetColorFromHex() {
table = new TableOfColor(new Locale(«ru»));
for (int i = 0; i < 10; i++) {
table.findNamedColorFromHex(hexes.get(i));
}
}
@Benchmark
@Fork(1)
public void testGetColorWithoutBucket() {
tableW = new TableOfColor();
for (int i = 0; i < 10; i++) {
table.findNamedColorWithoutBuckets(hexes.get(i));
}
}
Я специально выбирал 10 случайных цветов, так как при поиске одного цвета преимущество осталось бы за простым перебором. А так:
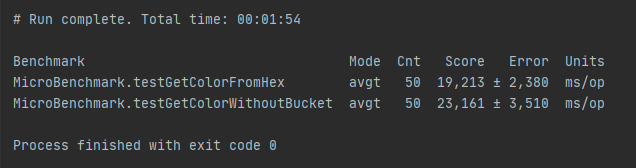
Преимущество на первый взгляд незначительно. Но что, если вынести создание таблицы в первоначальные настройки? Что будет вполне логично для массового поиска именованных цветов.
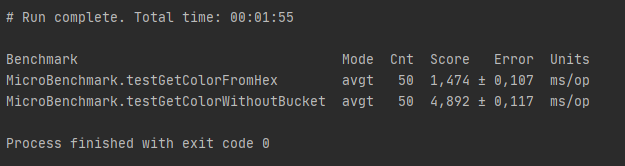
Как несложно заметить, теперь производительность лучше в 3 раза. Так что мои страдания были не напрасны.
Попытки протестировать получение данных с различных сайтов закончились баном уже на 5-й итерации( 1000-е обращение к сайту) и запредельно большими задержками ответа.
P.S.: Если тестируете библиотеку — делайте это в отдельном проекте. Я удалил из библиотеки все лишние неэффективные методы и теперь меня терзает мысль, что вещественных подтверждений проделанной работы теперь и нет вовсе. Кроме этой статьи.
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.